

We will be looking at these functions in more detail in the future. I have provided a few very brief examples using the cdf. All probabilities concerning \(X\) can be stated in terms of \(F\).If \(X\) is a discrete random variable whose minimum value is \(a\), then \(F_X(a)=P(X\le a)=P(X=a)=f_X(a)\).This makes sense since \(F_X(t)\) is a probability. The cdf, \(F_X(t)\), ranges from 0 to 1.\(F_X(t)\) is a nondecreasing function of \(t\), for \(-\inftyThe cdf of random variable \(X\) has the following properties:
#CDF AND PDF SOFTWARE#
They are just not always used since there are tables and software that help us to find these probabilities for common distributions. It does not mean that the cdf is not important for discrete random variables.
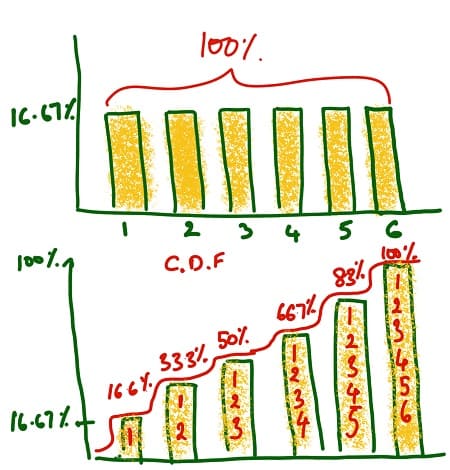
We do not focus too much on the cdf for a discrete random variable but we will use them very often when we study continuous random variables. The notation \(F_X(t)\) means that \(F\) is the cdf for the random variable \(X\) but it is a function of \(t\). The notation sometimes confuses students. The cdf is not discussed in detail until section 2.4 but I feel that introducing it earlier is better. The cdf is discussed in the text as well as in the notes but I wanted to point out a few things about this function. I hope to give you a reference.The cumulative distribution function (CDF or cdf) of the random variable \(X\) has the following definition:
#CDF AND PDF PDF#
The above example of Python processing PDF and CDF is all the content shared by the editor.

Plt.bar(bin_edges, hist/max(hist), width=width, color='#5B9BD5') The figure above shows the normalized pdf and cdf. This implementation needs to normalize pdf and cdf respectively. More often, it is necessary to put pdf and cdf together to better display the data distribution. The probability density function PDF upper plot is the derivative of the cumulative density function CDF lower plot This elegant relationship is illustrated here The default plot of the PDF answers the question How much of the distribution of a random variable is found in the filled area that is how much probability mass is there between. The figure above shows the cdf graph generated by two algorithms. Use seaborn's cumfreq() to draw cdf directly Use numpy's data processing function histogram() to generate pdf distribution data, and further generate cdf
#CDF AND PDF HOW TO#
The following describes how to use python to generate cdf: Sns.distplot(arr, kde=False, fit=stats.gamma, rug=True) The figure above shows the pdf generated by 3 algorithms. Using seaborn's distplot(), the advantage is that you can fit the pdf distribution and check the distribution type of your own data Using numpy's data processing function histogram(), you can generate pdf distribution data to facilitate subsequent data processing, such as further generation of cdf Use matplotlib's drawing interface hist() to directly draw the pdf distribution The following describes the method of using python to generate pdf:

For the distribution of data, there are two types of pdf and cdf. After getting the data, one of the most important tasks is to check the distribution of your data.


 0 kommentar(er)
0 kommentar(er)
